什么是满二叉树
如果一棵二叉树所有分支都存在左右子节点,且所有的叶子节点都在同一层,则成这棵树为满二叉树。

满二叉树a与非满二叉树b
什么是完全二叉树
一棵深度为K,有n个节点的二叉树,对树中节点按照从上至下,从左至右的顺序进行编号,如果编号为i(1<=i<=n)与满二叉树的编号为i的位置一致,则称此树为完全二叉树。总结:完全二叉树的先序遍历树满二叉树的子集。

堆排序代码
堆是一个完全二叉树。堆(heap)亦被称为优先队列(priority queue)。
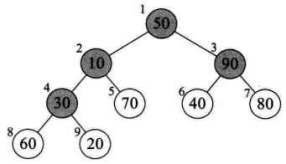
- 初始堆数组储存值是初始堆的先根遍历结果,如上图
int[] heap = {50, 10, 90, 30, 70, 40, 80, 60, 20};
- 第一个非叶节点下标=堆数组长度除/2-1,如上初始堆数组9/2-1=3,下标为3对应着30
package com.zlc.jzlc;
import java.util.Arrays;
public class HeapSort {
/**
* 获得该节点左子节点下标
*
* @param i 节点下标
* @return
*/
private int getLeft(int i) {
return 2 * i + 1;
}
/**
* 获得该节点右子节点下标
*
* @param i 节点下标
* @return
*/
private int getRight(int i) {
return 2 * i + 2;
}
/**
* 交换ij下标值
*
* @param arrays 数组
* @param i i下标
* @param j j下标
*/
private void swap(int[] arrays, int i, int j) {
int tmp = arrays[i];
arrays[i] = arrays[j];
arrays[j] = tmp;
}
/**
* 调整堆
*
* @param arrays 堆数组
* @param length 堆数组length
* @param i 子堆根节点下标
*/
private void ajustHeap(int[] arrays, int length, int i) {
int left = getLeft(i);//左孩子下标
int right = getRight(i);//右孩子下标
int big = i;//较大的节点下标
while (left < length || right < length) {//循环直到确定最终位置
if (left < length && arrays[left] > arrays[big]) {
big = left;
}
if (right < length && arrays[right] > arrays[big]) {
big = right;
}//确定较大键值的下标
if (i == big) {//如果该节点满足要求,则跳出循环
break;
} else {//否则与较大键值的孩子交换,并递归往下
swap(arrays, i, big);
i = big;
left = getLeft(i);
right = getRight(i);
}
}
}
/**
* 对一个完全二叉树建堆
*
* @param arrays 数组
* @param length 数组长度
*/
private void buildHeap(int[] arrays, int length) {
//从第一个非叶结点开始调整
//由于堆是完全二叉树,因此如果堆的总节点个数是偶数,则最后一个叶节点一定是其父节点的左孩子
//如果堆的总结点数是奇数,则非叶节点均包含两个孩子(扯远了)
int begin = length / 2 - 1;
for (int i = begin; i >= 0; i--) {
ajustHeap(arrays, length, i);//建堆的过程就是逐个调整的过程
}
}
/**
* 堆排序
*
* @param arrays 待排序堆数组,根先序遍历
*/
private void sort(int[] arrays) {
int length = arrays.length;
buildHeap(arrays, length);//建大顶堆
while (length > 1) {
swap(arrays, length - 1, 0);
length--;//将最大节点从堆中删除
ajustHeap(arrays, length, 0);//调整堆,只需调整第一个节点即可
//buildHeap(arrays, length);//建大顶堆
}
}
public static void main(String[] args) {
HeapSort heapSort = new HeapSort();
int[] heap = {50, 10, 90, 30, 70, 40, 80, 60, 20};
System.out.println(Arrays.toString(heap));
heapSort.sort(heap);
System.out.println(Arrays.toString(heap));
}
}